Seismic Refraction

Basic Concept

By exploiting the energy generated during global earthquake events, seismic-refraction techniques have played a pivotal role in identifying the macroscopic layers of deep Earth (Musset and Khan, 2000). Over the last several decades, the applications of seismic-refraction techniques have evolved from larger-scale investigations (e.g., earthquakes, seismotectonics, oil/gas, etc.) to smaller-scale surveys. Such near-surface applications image the subsurface using controlled seismic signals to assist environmental, engineering, or hydrogeologic investigations.

Seismic energy propagates through media as waves and, under certain conditions, undergoes critical refraction. A critically refracted seismic wave travels along acoustic interfaces and generates new waves that can be detected at the surface. The seismic-refraction method measures the time a seismic-energy pulse takes to travel from a source point to several receivers after being redirected by one or more subsurface interfaces. Depths to hydrogeologic contacts and types of geologic material can be estimated using data-based seismic-velocity discontinuities and magnitudes, respectively.

Conceptual diagram of seismic refraction showing seismic shot energy and refracted wave propagation through layers of variable seismic velocity — Schematic diagram of seismic wave propagation and refraction off earth layers of differing seismic velocity. (source USGS stock image)

Theory

Seismic waves are waves of acoustic energy that induce oscillations within, interact with, and are influenced by subsurface earth materials. Refraction methods are concerned with the compressional (P) and shear (S) seismic body waves, which travel within the interior of geologic bodies. These waves can be differentiated by how they affect the materials through which they travel. P-waves displace material in the direction parallel to their travel direction, whereas S-wave displacement is normal (i.e., perpendicular) to their travel direction.

P-wave propagation is analogous to a spring that is stretched and released along its longitudinal axis, and S-wave propagation resembles the movement of a sidewinder snake. Consequently, P-waves are faster, able to pass through all liquids and solids, and more easily identified. Thus, P-waves are predominately used in near-surface refraction surveys and the focus of this discussion. Though S-wave refraction surveys are rare, their efficacy for evaluating unconsolidated materials was demonstrated by Ellefsen and others (2005).

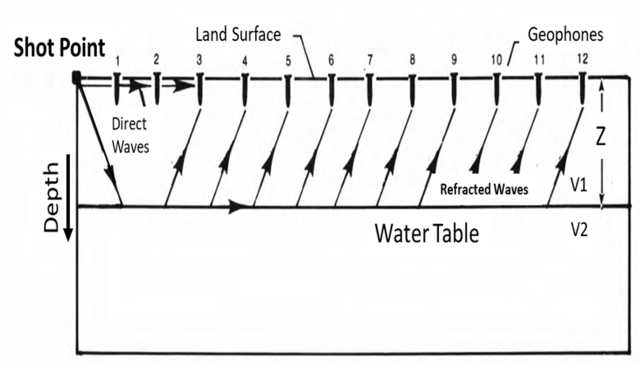
In homogeneous media, a seismic wave travels semispherically such that the instantaneous extent of seismically influenced material (i.e., wavefront) has a radius that increases with propagation. Waves can be described by their rays, each of which travels perpendicular to the wavefront and arrives at an acoustic interface at an angle of incidence (Θ_i). This angle, which is between 0° and 90°, is formed by an arriving (i.e., incident) ray and normal to the interface.

Seismic rays travel from a surface-source point to a receiver as either a direct-, reflected-, or refracted ray. The direct ray travels just beneath the surface toward the receiver. Reflected rays, which are most common, are immediately redirected to the surface by the interface. The critically refracted ray originates from the ray that arrives at the critical angle of incidence (Θ_ic). It is deflected away from normal and travels along the bottom of the interface.

Seismic rays travel through a medium at some seismic velocity that depends on wave type and the material’s elasticity and density. In a two-layered model containing a horizontally planar interface, critical refraction occurs only if the lower-layer velocity exceeds the upper-layer velocity. The critically refracted ray travels at the lower-layer velocity while inducing head waves in the upper layer. The newly generated rays leave the interface at an angle that is equal and opposite to Θ_ic (Musset and Khan, 2000).

Multiple receivers (i.e., geophones) are typically employed in a line along the land surface to detect the seismic energy at each point over time. Typically, the first arrivals of each ray at each geophone are picked and, because they contain sufficient information, used to determine the depths to acoustic interfaces. Assuming the survey design and layer-velocity conditions are met, the geophone closest to the seismic source will detect the direct ray first.

The symmetry between the critical angle of incidence and angle of refraction produces two effects. Refracted rays 1) are only detectable at/beyond a critical distance (X_c) away from the source, and 2) travel the same distance in the upper, lower-velocity layer. Thus, as the source to receiver distance increases, the refracted ray travels further in the lower, higher-velocity layer. Geophones that are at/beyond the crossover distance (X_cross ) from the source will detect refracted rays first as they have overrun the direct ray.

The reflected rays travel only in the upper layer and, thus, are always the last to arrive at a receiver. Consequently, reflected rays are not considered in the refraction survey. Ray path distinction is not possible in the field, and it is inferred by graphing the field data. Such analysis includes generating a time-distance plot, where the travel times of the first arrivals are picked and plotted against the distance between the geophone and source (Haeni, 1988).

Applications

Seismic-refraction surveys employ arrays or transects of geophones positioned on the land surface at known locations with specific distances from the active-source shot point(s). Data can be improved by using multiple shot points, which are often offset near to, far from, and centered in between both ends of the survey line. Site-specific (i.e., wave type, energy magnitude) seismic signals can be actively transmitted into the subsurface by explosions, vibrators, accelerated-weight drops, or hammers.

Once triggered by the shot, a seismograph continuously records the magnitude and direction (i.e., positive or negative) of the seismic energy at each corresponding geophone. The raw data record (i.e., seismogram) consists of “wiggle” traces that show amplitude variations, which signify changes in seismic energy magnitude, as a function of time. The times corresponding to the arrivals of seismic energy are picked based on significant shifts in trace amplitude.

The seismic velocities of the subsurface layers can be estimated by analyzing the slopes of the lines that form by graphing the first arrivals in time-distance plots. Furthermore, refracted rays have specific paths that depend on the seismic-layer velocities as well as the thickness of the upper layer(s). Because critical- and crossover distances depend directly subsurface parameters, layer thicknesses can be determined using relatively simple calculations (Haeni, 1988).

When dealing with multiple-layer models, there is a critical ray for each interface that depends upon the velocities above and below the interface. Because the ray paths down to an interface depend upon the thicknesses and seismic velocities of all the layers above it, computation becomes more involved (Mussett and Khan, 2000). These computations have been facilitated by use of computer programs for processing and interpreting seismic-refraction data.

Numerous interpretation methods exist and are generally subdivided based on their approach to finding a layered solution. The first is the refractor-interface modeling approach, which defines the depths and positions of refracting layers. This is typically done using the delay-time method (Pakiser and Black, 1957) and ray-tracing techniques that help delineate dipping and undulating layers (Mussett and Khan, 2000). The second, more complicated analysis is solved by inverse methods and generates two- or three-dimensional velocity tomograms.

Tomographic methods generally use a starting model of the velocity field, array geometry, and first-arrival travel-time data. The inversion process iteratively updates the velocity profile to minimize an objective function that assesses model misfit between measured and predicted values. Slowness, which, being the inverse of velocity, has units of time per distance, is sometimes used instead because it may be computationally easier for inversion. Detailed descriptions of tomographic seismic methods are provided by Kirsch (2006).

The refractor-interface modeling approach falters if any of the following three conditions exist. 1) A layer with a seismic velocity lower than that above it will not be identified, and the depths to underlying layers will be overestimated. 2) Insignificant seismic-velocity contrasts or gradational contacts between layers can leave them undifferentiated. 3) A thin layer within a sequence that has similar or increasing thicknesses with depth will be hidden, and the depths to underlying layers will be erroneous.

Advantages of the tomographic method over the refractor-interface approach are that a priori constraints can be incorporated into the model to improve the results. In addition, tomographic inversions are not limited by the velocity inversion, gradual changes, and blind-zone problems that can be detrimental to more traditional methods. However, one possible limitation is that the solution is often smoother and more gradational, even when discrete layers are appropriate.

Dataset resolution and depth of investigation (DOI) are typically related to the locations/spacing of geophones and shot point(s). Generally, increasing array density increases resolution, and DOI is increased by increasing survey-line length and/or signal magnitude. However, certain conditions (e.g., lateral seismic-velocity variations, vertical velocity variations within a single unit, ambient noise) may introduce erroneous signals and complicate interpretations. Thus, some knowledge prior to surveying may be beneficial, so arrays can be planned according to estimated subsurface structure and survey goals such as the following:

Determining the depth to the water table
Mapping the bedrock surface
Determining the depths to stratigraphic contacts
Estimating soil type
Mapping sink holes, abandoned mines, voids, etc.
Identifying structural features (e.g., faults and fractures)
Detecting intrusive geologic bodies
Estimating rock rippability (i.e., ease with which it can be mechanically excavated)

Image of seismic refraction hammer source field data acquisition — A seismic refraction survey conducted using the hammer and plate method. (source USGS)

Examples/Case studies

Adelinet, M., Domínguez, C., Fortin, J., and Violette, S., 2018, Seismic-refraction field experiments on Galapagos Islands: A quantitative tool for hydrogeology: Journal of Applied Geophysics, v. 148, p. 139-151, doi:10.1016/j.jappgeo.2017.10.009.

Abstract: Due to their complex structure and the difficulty of collecting data, the hydrogeology of basaltic islands remains misunderstood, and the Galapagos islands are not an exception. Geophysics allows the possibility to describe the subsurface of these islands and to quantify the hydrodynamical properties of its ground layers, which can be useful to build robust hydrogeological models. In this paper, we present seismic refraction data acquired on Santa Cruz and San Cristobal, the two main inhabited islands of Galapagos. We investigated sites with several hydrogeological contexts, located at different altitudes and at different distances to the coast. At each site, a 2D P-wave velocity profile is built, highlighting unsaturated and saturated volcanic layers. At the coastal sites, seawater intrusion is identified and basal aquifer is characterized in terms of variations in compressional sound wave velocities, according to saturation state. At highlands sites, the limits between soils and lava flows are identified. On San Cristobal Island, the 2D velocity profile obtained on a mid-slope site (altitude 150 m), indicates the presence of a near surface freshwater aquifer, which is in agreement with previous geophysical studies and the hydrogeological conceptual model developed for this island. The originality of our paper is the use of velocity data to compute field porosity based on poroelasticity theory and the Biot-Gassmann equations. Given that porosity is a key parameter in quantitative hydrogeological models, it is a step forward to a better understanding of shallow fluid flows within a complex structure, such as Galapagos volcanoes.

Goodwin, J., Meixner, T., McAlpine, S., and Nicoll, M., 2016, Estimating cover thickness using seismic refraction in the southern Thomson Orogen — An UNCOVER application: ASEG Extended Abstracts, v. 2016, no. 1, 4 p., doi:10.1071/ASEG2016ab130.

Abstract: The Southern Thomson Project was established to develop a better understanding of the geology and mineral potential of the southern Thomson Orogen. One way in which the Southern Thomson Project is improving this understanding is through the collection of seismic refraction data at 16 greenfields sites to assess the cover thickness (i.e. the amount of regolith and sedimentary basin cover overlying the basement geology). Seismic refraction data were collected using a standard linear array with 48 geophones and a 40 kg propelled weight drop as the energy source. An estimate of the cover thickness was produced from the refraction data using the time-term inversion method. This resulted in the creation of a three-layer model for each site, which accounts for the layers associated with the regolith, sedimentary basin cover and the basement geology.

Nolan, J.J., Sloan, S.D., Broadfoot, S.W., McKenna, J.R., and Metheny, O.M., 2011, Near‐surface void identification using MASW and refraction tomography techniques: SEG Technical Program Expanded Abstracts 2011, p. 1401-1405, doi:10.1190/1.3627464.

Abstract: natural or anthropogenic dissolution features, illegal cross‐border tunnels, or abandoned mines. Detection of these voids using geophysical methods has often proven difficult due to multiple factors including depth‐to‐diameter ratio, lack of resolution, non‐uniqueness, etc. Experiments were conducted at a test site with a known subsurface void to determine the capability of multiple near‐surface seismic methods as applied to void detection. In this study, refraction tomography and multichannel analysis of surface wave methods successfully identified a man‐made void approximately three meters deep. Results of these experiments correlated well with the expected results, exhibiting decreased velocity, the absence of seismic ray coverage, and a high shear‐wave velocity halo above the void.

Pegah, E., and Liu, H., 2016, Application of near-surface seismic refraction tomography and multichannel analysis of surface waves for geotechnical site characterizations: A case study: Engineering Geology, v. 208, p. 100-113, doi:10.1016/j.enggeo.2016.04.021.

Abstract: In this case study two geophysical methods based on seismic waves were employed to evaluate the geotechnical properties of the soil deposits at a site for a planned wind farm. Regional geological information shows that the study area is mainly covered by recent alluvium, which is classified as a mixture of fine sand and gravel. Twenty five seismic refraction surveys were carried out in the study area. The acquired shot gathers were processed, from which primary wave (P-wave) and shear wave (S-wave) velocities were derived. The P-wave velocities were obtained by using the Seismic Refraction Tomography method (SRT) while the S-wave velocities were extracted by utilizing the Multichannel Analysis of Surface Waves (MASW) technique, which is established based on the dispersion characteristics of Rayleigh waves. Seismic hazard at the site was evaluated according to the Iranian code using the measured S-wave velocities, and the friction angles of the soil deposits were approximated using an empirical method and by making use of Jaky's formula for earth pressure at rest, which yielded similar values. The deformation properties of the foundation soil were also estimated based on the correlations between seismic wave velocities and elastic properties of soil as well as Janbu's formula for soil modulus. The findings of this study may serve as references for economic and non-destructive geotechnical site characterizations using seismic-wave methods.

Srinivas, G.S., Shankar, P., Kumar, K., Trupti, S., Kishore, P., Srinivas, K., and Seshunarayana, T., 2018, Application of Shallow Seismic Studies for Civil Engineering Applications: A case study from Chennai city, Tamilnadu: The Journal of Indian Geophysical Union, v. 22, no. 3, p. 286-291.

Abstract: Shear wave (VS) and P-wave (VP) velocities were estimated for the evaluation of the sub-surface structure along four profiles at CSIR-SERC Campus in Chennai city to aid in the structural design for a proposed high rise building. These velocities are essential parameters for determining the dynamic properties of soil in the shallow subsurface. Dynamic properties, thickness of soil, depth to basement and the associated in-homogeneities such as fractures, joints, voids and shear zones, play a very important role in design and construction of civil structures. Multichannel analysis of surface waves (MASW) and refraction methods were used for the estimation of VS and VP respectively to decipher the subsurface structure in detail. From

the Seismic velocity-depth sections, the near surface distribution of rocks, soils and their physical properties were determined to characterize the site conditions. The results indicate a three layered structure with P-wave velocities of 400-500 m/s, 2700-3100 m/s and 5300-5500 m/s and S-wave velocities of >200 m/s, 200 to 300 m/s and >400 m/s up to a depth of 30 m. The obtained results are well correlating with the available borehole lithological data. These results are helpful in civil engineering applications in estimation of elastic properties, depth to bedrock and useful in planning of high rise structures.

References

Haeni, F.P., 1988, Application of seismic-refraction techniques to hydrologic studies: U.S. Geological Survey Techniques of Water Resources Investigations, book 2. Chap. D2, 86 p., available at: https://pubs.usgs.gov/twri/twri2d2/pdf/twri_2-d2.pdf.

Kirsch, R., 2006, Groundwater Geophysics A tool for hydrogeology: New York, Springer, 500 p.

Mussett, A.E., and Khan, M.A., 2000, Looking into The Earth: An Introduction to Geological Geophysics: New York, Cambridge University Press, 470 p.

Pakiser, L.C., and Black, R.A., 1957, Exploring for ancient channels with the refraction seismograph: Geophysics, v. 22, no. 1, p. 32-47, doi:10.1190/1.1438336.